Solving Mastermind with Maximum Entropy

The rules are standard: the computer picks a secret code of 4 colored pegs from 6 options (repeats allowed). After every guess, you receive feedback: Black for correct color and position, White for correct color but wrong position.

The "Best Guess" suggestion uses maximum entropy to find the most efficient next move. When colors remain interchangeable, many patterns provide equivalent information—the advisor groups these by their entropy value.

But not all guesses are equally informative.

With 6 colors and 4 positions, there are 6⁴ = 1296 possible codes. Each bit of information halves the search space. Starting from 1296 candidates, we need roughly log₂(1296) ≈ 10.34 bits to narrow it down to one. That's about 10 halvings:

Different guesses split the remaining possibilities in very different ways. The goal is to find the guess that maximizes this "cut," eliminating the largest number of impossible codes.

With 4 positions, there are 15 theoretically possible feedback combinations:

Not all of these can actually occur. The pattern 3 black, 1 white is impossible. If three colors are in the correct positions, the fourth must also be correct or entirely wrong. Other patterns become impossible depending on the specific guess. For example, guessing all the same color can never produce any white pegs.

The efficiency of a feedback pattern depends heavily on your guess. Consider the very first turn:

• Guessing ●●●● (All Different): An empty feedback eliminates 4 colors entirely. Leaves only 2⁴ = 16 candidates.
• Guessing ●●●● (All Same): An empty feedback eliminates only 1 color. Leaves 5⁴ = 625 candidates.

We need a metric that tells us which guess, on average, provides the best reduction across all possible feedback it might receive.

The most efficient guess spreads the remaining possibilities evenly across all feedback patterns. If candidates split into equal-sized buckets, we make progress regardless of which feedback we get.

Entropy measures this evenness:

where x represents each possible feedback pattern, and p(x) is the probability of receiving that feedback:

Higher entropy means more even distribution. The guess with maximum entropy gives us the most information on average.

At each turn, the algorithm evaluates all 1296 possible guesses and sorts them by how much they're expected to reduce the remaining search space.

For each candidate guess:

1. Simulate the feedback it would generate against every remaining possible secret code
2. Group the remaining codes by their feedback pattern (e.g., how many would return 2 black, 1 white?)
3. Calculate the entropy of this distribution

The algorithm sorts all guesses by entropy. You can pick any guess, but the top one maximizes expected information gain.

Tested against all 1296 possible secret codes, the algorithm solves the game in an average of 4.42 guesses:

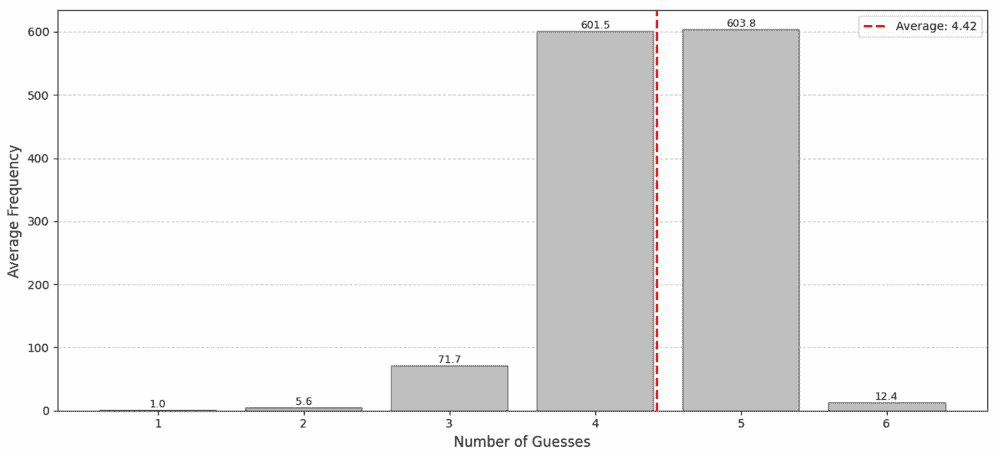
Full results and calculations are available in the Jupyter notebook.

Maximum Entropy helps pick guesses that give the most information on average. It’s not the only way to play. Donald Knuth's "Minimax" strategy focuses on the worst-case and can always win in five moves.

Try playing with the advisor above and see what patterns you notice. I found it interesting that initial guess patterns are in the same order as poker hands:

This article was inspired by 3Blue1Brown's video on solving Wordle with information theory.